Fourier Optics

Fourier transform

General sine function:

$$ \begin{equation} y(x) = A \sin(\frac{2 \pi}{T} x + \varphi) \end{equation} $$

Where $A$ is the amplitude, $T$ is the period, and $\varphi$ is the phase.

We can also say that $T$ is the wavelength $\lambda$, and $f = \frac{1}{\lambda} = \frac{1}{T}$ is the frequency.

So another general form of the sine function is:

$$ \begin{equation} \begin{aligned} y(x) &= A \sin(\frac{2 \pi}{\lambda} x + \varphi) \newline &= A \sin(2 \pi f x + \varphi) \newline \end{aligned} \end{equation} $$

So for 1D sine wave, $A$, $f$ (or $\lambda$), and $\varphi$ are the three crucial parameters that can describe the wave.

The fourier transform is a decomposition process: Any periodic function can be decomposed into a series of sine and cosine functions with different amplitudes, frequencies and phases.

A visualization of the relationship between the time domain and the frequency domain of a function, based on its Fourier transform. From Wikipedia.

Mathematically,

$$ \begin{equation} f(x) = \frac{A}{2} + \sum_{m=1}^{\infty} A_{m}\cos(\frac{2 \pi mx}{\lambda}) + \sum_{m=1}^{\infty} B_{m}\sin(\frac{2 \pi mx}{\lambda}) \end{equation} $$

where $A_{m}$ and $B_{m}$ are the amplitudes of the cosine and sine functions, respectively.

More sinusoid functions with higher frequencies will destribe the function better. The highest frequency in the decomposition will be refered to as the Nyquist frequency.

Example of convergence to a somewhat arbitrary function. From Wikipedia.

And the fourier transform can be fully converted:

$$ f(x) \xrightarrow[F.T.]{\mathcal{F}} F(k) \xrightarrow[Inverse F.T.]{\mathcal{F}^{-1}} f(x) $$

Fourier transform allows representing any periodic function as a linear combination of sinusoids. The new variables it uses will be: amplitudes, frequencies, and phases.

Fourier transform and the lens

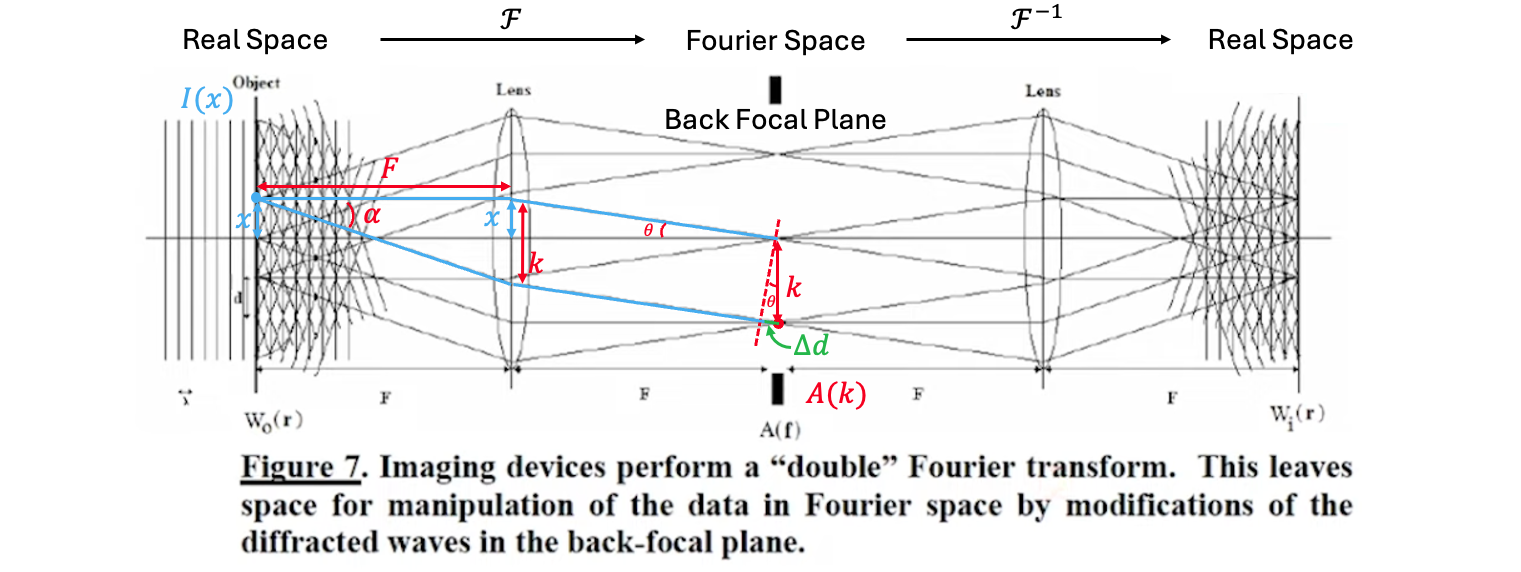
$$ \begin{equation} \tan(\theta) = \frac{x}{F} \approx \sin(\theta) \end{equation} $$

where $F$ is the focal length of the lens, and $x$ is the distance between one small point and the center of the sample/object, which represents certain featrues of the sample (grating period).

Because the electrons which run parallel to the optical axis and those scattered by the sample have the same frequency (image spacial frequency $\neq$ wave frequency), they can interfere with each other by the delay of $\Delta d$, which contributes to some certain patterns in the fourier space (Back Focal Plane). Say the distance between the center of the diffaction pattern and certain feature in the diffaction pattern is $k$, and its amplitude is $A(k)$.

$$ \begin{equation} \Delta d = k \sin(\theta) \approx k \frac{x}{F} \end{equation} $$

So the object can be decomposed into:

$$ \begin{equation} I(x) = \sum A(k) \cos(\frac{2\pi}{\lambda} \times n \Delta d) \end{equation} $$

where $n$ is the refractive index.

Then:

$$ \begin{equation} \begin{aligned} I(x) &= \sum A(k) \cos(\frac{2\pi n}{\lambda} \times \frac{kx}{F}) \newline &= \sum A({\color{blue}k}) \sin({\color{blue}k} {\color{red}x} \times \frac{2\pi n}{\lambda F} + \frac{\pi}{2}) \end{aligned} \end{equation} $$

Obviously, the above equation is the Fourier transform of the object.

So, the spacial frequency $f_{S}$ can be represented by:

$$ \begin{equation} f_{S} = \frac{2\pi kn}{\lambda F} = \frac{2\pi n}{\lambda F} \times k \end{equation} $$

We can also try to calculate the Abbe Diffraction Limit:

When $k$ is equal to the radius of the lens (or the size of the back aperture), the spacial frequency is the highest, and the $\alpha$ angle reaches the maximum.

$$ \begin{equation} k_{max} = F \tan \alpha_{max} \approx F \sin \alpha_{max} \end{equation} $$

where $\alpha_{max}$ is the half angle of the maximum cone of light that can enter or exit the lens.

$$ \begin{equation} \begin{aligned} N.A. &= n \sin \alpha_{max} \newline &= \frac{n k_{max}}{F} \end{aligned} \end{equation} $$

So the highest spacial frequency is:

$$ \begin{equation} \begin{aligned} f_{S_{max}} &= \frac{2\pi n}{\lambda F} \times k_{max} \newline &= \frac{2\pi}{\lambda} \times N.A. \end{aligned} \end{equation} $$

The Abbe Diffraction Limit tells us that when the peak of one wave falls on the minimum of another adjacent wave (phase difference is $\pi$), we can exactly distinguish the two waves. So the minimum distance between two points that can be distinguished is:

$$ \begin{equation} \Delta x_{min} = \frac{\pi}{f_{S_{max}}} = \frac{\lambda}{2 N.A.} \end{equation} $$

The above is a simple derivation of the Abbe limit.

2D/3D Fourier transform

Representation of images in real space

• Any images consist of pixels
• Pixels are represented by coordinates and intensity values.

We can also represent images by the linear combination of other images. These images are called base images (base vectors). So an image can be represented by the sum of these base images with certain coefficients.

Fourier decomposition of 2D images

The Fourier transform of some real-space base images:

Here the size of the dots is increased for better visualization.

When we decompose a $8 \times 8$ real-space image, we can get 64 basis images, which correspond to amplitudes and phases of each frequency component.

Fourier transform in 2D images

When we perform the Fourier transform of an image, we can get the amplitude and phase spectrum at the same time.

3D Fourier transform

Fourier Transform can be generalized further into 3D or ND spaces. Like the examples in 1D and 2D, the 3D fourier transform is also a decomposition process, which can be represented by the sum of multiple 3D base waves in volume.

Multiple 3D base waves in volume

3D Fourier transform

References

• Lecture 6 - Cryo-Electron Microscopy - Fourier transform, image formation, CTF
• Fourier transforms in cryo-EM | Convolution, Gaussian filters, Fourier Shell Correlation, FFT